פרק קודם:

מה נלמד

• מהי רקורסיה
• תנאי עצירה
• import
• Call stack

רקורסיה

הגדרת רקורסיה היא -

פרוצדורה או הגדרה שחוזרת על עצמה

פרוצדורה בעניין שלנו זו פונקציה, כפי שלמדנו בפרק הקודם.
זו בעצם פונקציה שחוזרת על עצמה!

איטרציה מול רקורסיה

האם זו רקורסיה?

1
2
3
4
5

def func():
    pass

while True:
    func()

לפי ההגדרה בלבד הדוגמא הזו יכולה להיות רקורסיה כי זו פונקציה שחוזרת על עצמה ולפי תנאי הלולאה - רצה לעד.

פונקציה רקורסיבית

בתכנות - רקורסיה זה קיצור לפונקציה רקורסיבית.
פונקציה רקורסיבית היא פונקציה שקוראת לעצמה מתוך גוף הפונקציה.

רקורסיה פשוטה תיראה כך:

1
2
3
4
5
6
7

def func(n):
    if n < 1:
        return 0
    print(n)
    return func(n - 1)

func(5)

מה שיודפס מהפונקציה הזו:

1
2
3
4
5
6

5
4
3
2
1
0

מה שקורה פה מתואר בדיאגרמה הבאה:

אנחנו מתחילים מלמעלה ויורדים למטה וחוזרים בסוף.
כל שלב אנחנו בודקים את תנאי העצירה.
אם המספר קטן יותר מ-1 הפונקציה מחזירה 0.
אם לא - ממשיכים לפונקציה הרקורסיבית עם מספר נמוך יותר ב-1.

עד שלבסוף אנחנו מגיעים לתנאי עצירה שלנו, וחוזרים למעלה.
כל השלבים נקראים מחסנית קריאות או call-stack.

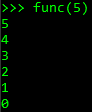
למה אני מקבל גם 0 בפלט?

מחסנית קריאות

מחסנית קריאות זהו מבנה נתונים בתוכנה ששומר את סדר הקריאות של פונקציות.
יש לזה כמה שמות נוספים:

• מחסנית ריצה
• מחסנית תוכנה
• מחסנית הרצה
• מחסנית מכונה

לעיתים מכונה גם “המחסנית”.

בקריאה לפונקציה הריצה שלה נשמרת.

1

func(5)

ניתן לראות במחסנית כתיעוד לריצה של פונקציה על מנת שכשתוכנה מסיימת את הפונקציה היא תוכל לחזור לנקודה האחרונה שהיא רצה ממנה.

המחשה באנימציה הבאה:

בתוכנה Visual Studio Code ניתן לראות את סדר הקריאות ב-Debug:

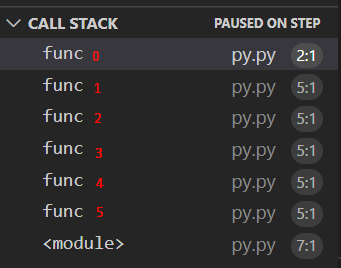
במקרה שלנו הרצת הקוד הרקורסיבי תשמור במחסנית כל ריצת func() עם הפרמטר n.
ואז כשהריצה חוזרת אחורה - כל פונקציה “יוצאת מהמחסנית” בסדר ההפוך שהן נכנסו - האחרון שנכנס הוא הראשון יוצא.
או במילים אחרות LIFO - Last in First out.

תנאי עצירה

פונקציה רקורסיבית מורכבת מ-2 חלקים:

1. הלוגיקה של הפונקציה - חישוב, או ביצוע פעולה כלשהי.
2. תנאי עצירה המגדיר את גבולות הפונקציה.

בפסודו קוד זה נראה כך:

1
2
3
4

פונקציה: 
    תעשה X
    אם תנאי כלשהו קרה - תצא
    אם לא תקרא לפונקציה

מה קורה במידה ואין לנו תנאי עצירה או שטעינו בו?
הריצו את קטע הקוד הבא:

1
2
3
4

def func(n):
    return func(n-1)

func(10)

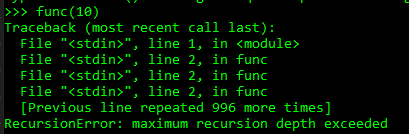
קיבלנו שגיאה מפייתון על כך שהגענו ל”עומק” המקסימלי של הפונקציה.

זה מלמד אותנו על כך שאין דבר כזה רקורסיה אינסופית.

למה אין דבר כזה רקורסיה אינסופית?
תחשבו לפני שאתם קוראים את הקטע הבא.

Answer

זוכרים את הcall-stack?

נניח שהגבלנו את הstacktrace ל5.
אם הרקורסיה שלנו גדולה מ-4 אנחנו נמלא את כל המחסנית ולא יהיה מקום לעוד קריאות של פונקציות.
ובמידה והרקורסיה שלנו גדולה מ-5, אנחנו נקבל שגיאה כזו!.

לקריאה נוספת:
Wikipedia - callstack

תנאי עצירה הוא החלק הכי חשוב ברקורסיה כי תנאי עצירה שגוי ייפגע בפונקציונליות ויכול ליצור שגיאות שקשה למצוא!

כל קריאה נוספת לפונקציה נכנסת “עמוק” יותר לסדר הקריאות.
וככל שזה עמוק יותר כך גם זה “יקר” יותר.

לעיתים הקריאות של הקוד חשובה ולכן נוכל “לפצל” רקורסיות ולבנות אותן עם לולאות.
אני מוצא קריאות רקורסיביות פחות קריאות מכיוון שמדובר באלגוריתמים יחסית מורכבים, אבל זה לא הופך אותך לפחות יעילים.

דוגמא לשימוש ברקורסיה

רקורסיה היא לא הדבר המועדף על מתכנתים, הרבה מהן מעדיפים לממש בצורה איטרטיבית.
“Iterative” או “Iteration” - חזרה על פעולה.
כאשר אומרים “בצורה איטרטיבית” בד”כ מתכוונים ללולאה.
כעת נראה דוגמא למתי רקורסיה יכולה לעזור לנו.

עצרת

עצרת זוהי מכפלה של סדרה יורדת ב1.
5! = 5 * 4 * 3 * 2 * 1

1
2
3
4
5
6
7

def Factorial(n):
    if n == 1:
        return 1 
    else:
        return n * Factorial(n - 1)

print(Factorial(5))

כל מה שאנחנו עושים זה מכפילים עד שמגיעים לתנאי עצירה שלנו.

1. האם אתם יכולים לזהות את תנאי העצירה?
2. האם אתם מזהים בעיה בפונקציה הזו?

1
2
3
4
5
6
7

def Factorial(n):
    if n <= 1:
        return 1 
    else:
        return n * Factorial(n - 1)

print(Factorial(5))

פיבונאצ’י

זוכרים את סדרת פיבונאצ’י מפרק 6?
כעת נבחן את המימוש של אותו אלגוריתם בצורה רקורסיבית.

1
2
3
4
5
6
7
8

def RecursiveFibonacci(times):
    if times <= 1:
        return 1
    return RecursiveFibonacci(times - 1) + RecursiveFibonacci(times - 2)

solveFor = int(input('Choose index for fibonacci sequence: '))
result = RecursiveFibonacci(solveFor)
print(f'Solved for {result}')

בדוגמא הזו אנחנו קוראים לפונקציה פעמיים למה?

כי פיבונאצ’י מורכב מחיבור של שני המספרים הקודמים לו לכן בכל איטרציה אנחנו מחשבים את המספרים הקודמים.
הפונקציה ממומשת בצורה מאוד פשוטה אך היא לא הכי יעילה כי עבור כל מספר אנחנו צריכים לחשב את המספרים הקודמים.

תנסו לשחק עם הפונקציה ולתת לה מספרים שונים: 10, 20, 50, 500.

מהי ההגבלה של הרקורסיה?

בעזרת הקוד הפשוט הזה אפשר לבדוק מהו הגבול הרקורסיבי של פייתון במחשב:

1
2

import sys
print(sys.getrecursionlimit())

כשאני הרצתי את הקוד יצא:

1
2
3
4
5
6

Python 3.9.0 (tags/v3.9.0:9cf6752, Oct  5 2020, 15:34:40) [MSC v.1927 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> import sys
>>> print(sys.getrecursionlimit())
1000
>>>

תנסו בעצמכם ליצור רקורסיה יותר גדולה מהמספר שייצא לכם ותראו מה קורה!

היכרות עם import

כדי להקל עלינו ועל השימוש בפונקציות שכבר מומשו פייתון מציעה כלי שנקרא מודולים - Modules.
מודול הוא פונקציות המאוגדות ביחד - האיגוד הזה נקרא חבילה.
בעזרת החבילות ניתן לייצר פונקציות או לייבא.
ה-import היא מילת מפתח המייבאת מודולים.

כפי שראינו בפרק הראשון ,הפקודה pip שמנהלת חבילות, ונותנת את האופציה להתקין חבילות אחרות.
בפרק 14 נכיר את המודולים יותר לעומק.
אך לעת עתה הזכרתי את ה-import כי השימוש של זה יילך וייגדל.

תרגילים

1. כתבו רקורסיה המדפיסה את כל האיברים השלמים עד מספר מסוים שהמשתמש בחר.
   למשל עבור 5 זה ידפיס: 1, 2, 3, 4, 5.

2. כתבו פונקציה רקורסיבית שמקבלת מערך מספרים כקלט ומחזירה את ההמספר הנמוך ביותר שכל המספרים במערך מתחלקים בו.
   למשל עבור [2, 3, 4] הפונקציה תחזיר 12.

3. כתבו פונקציה רקורסיבית המקבלת רשימה והופכת אותה.
   למשל רשימה 1,2,3 תודפס הפוך: 3,2,1.

4. ממשו חיפוש בינארי Binary search בעזרת פונקציה רקורסיבית.
   על הפונקציה לקבל רשימה מסודרת ולחפש אלמנט שנותנים לו.

1
2
3
4
5
6
7
8
9

def BinarySearch(list, numToFind):
    pass


list = [2,4,6,8,9,10,11,13]
found = BinarySearch(list, 6)

if found:
    print("Found element!")

מהו חיפוש בינארי?
חיפוש בינארי הוא אלגוריתם לחיפוש אשר “מפצל” את הרשימה לשניים עד שהוא מוצא או לא מוצא את המספר.
במידה ולא מצאנו אנחנו ממשיכים לפצל עד שנמצא!

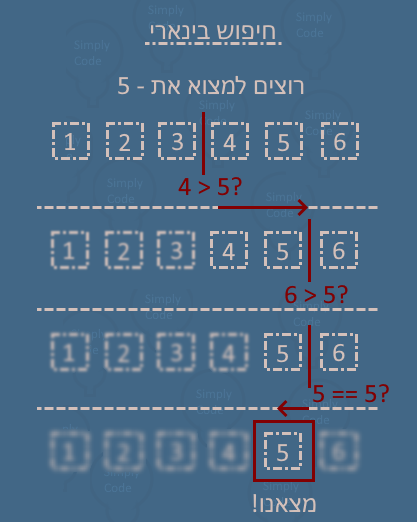
בתמונה כשפיצלנו מס’ אי זוגי הלכנו לאיבר הגבוה יותר, ז”א במקום 5 לקחנו את 6 והמשכנו לבדוק.
לעיתים האלגוריתם יכול ללכת למספר התחתון במקום העליון.

5. עליכם לכתוב פונקציה המוצאת את המספר הקטן ביותר בעץ בינארי.
   עץ בינארי הוא עץ שיש בו לכל היותר 2 ענפים.

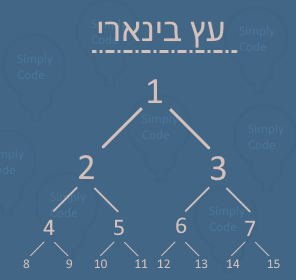
את העץ אני אגדיר בעזרת רשימות, סדר האיברים:

1. מספר
2. רשימה
3. מספר 2
4. רשימה 2

למשל עץ עם 2 ענפים 1,2 ו3:

1

tree = [1,[2,[],3,[]]]

זאת אומרת ענף עם בן אחד יהיה בעל רשימה של 2 אלמנטים.
ו-2 ענפים יהיו 4 אלמנטים.

להלן קוד שניתן להיעזר בו:

1
2
3
4
5
6
7
8
9
10
11
12

def Minimum(tree):
    return 0

minToFind = -90
treeToFindMin= [1,[2,[-5,[40,[],-25,[]]],3,[9,[-20,[],100,[]], minToFind,[5,[],3,[]]]]]

minFound = Minimum(treeToFindMin)

if minFound == minToFind:
    print("Good job!")
else:
    print("Oops, try again")

1
2
3
4
5
6
7
8
9

def RecursivePrint(number, limitNumber):
    print(number, end = ' ')
    number = number + 1

    if number <= limitNumber:
        RecursivePrint(number, limitNumber)

limit = int(input('Pick a limit number: '))
RecursivePrint(1, limit)

1
2
3
4
5
6
7
8

def RecursivePrint(number, limitNumber):
    print(number, end = ' ')
    number = number + 1

    if number >= limitNumber:
        return
    else:
        RecursivePrint(number, limitNumber)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def FindLeastCommonNumberMultiplier(numberList, allMultilperNumber=0):
    last = max(numberList)
    allMultilperNumber = allMultilperNumber + last

    areAllMultiplied = True

    for num in numberList:
        areAllMultiplied = areAllMultiplied and (allMultilperNumber % num == 0)

    if areAllMultiplied:
        return allMultilperNumber
    else:
        return FindLeastCommonNumberMultiplier(numberList, allMultilperNumber)


myNumbers = [55, 20, 30, 4]
print(FindLeastCommonNumberMultiplier(myNumbers))

1
2
3
4
5

areAllMultiplied = True

for num in numberList:
    areAllMultiplied = areAllMultiplied and (allMultilperNumber % num == 0)

1
2

if all(counter % num == 0 for num in arr):
    return counter

1
2
3
4
5
6
7
8
9
10
11
12
13

def Reverse(list: list, currIndex=0):
    if currIndex == len(list):
        return list

    reverseIndex = -1
    last = list[reverseIndex]
    list.insert(currIndex, last)
    list.pop()
    return Reverse(list, currIndex + 1)


arr = ['H', 'e', 'l', 'l', 'o']
print(Reverse(arr))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def BinarySearch(list, toFind):
    return __BinarySearch(list, toFind, 0, len(list)-1)


def __BinarySearch(list, toFind, low=0, high=0):
    if high >= low:
        mid = (high + low) // 2

        print(f'Searching Index {mid}, num: {list[mid]} == {toFind}')
        if list[mid] == toFind:
            return True
        elif list[mid] > toFind:
            return __BinarySearch(list, toFind, low, mid - 1)

        else:
            return __BinarySearch(list, toFind, mid + 1, high)
    else:
        return False


myList = [1, 2, 3, 4, 5, 6]
toFind = 5
found = BinarySearch(myList, toFind)
print(found)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

def Minimum(tree):
    return __Minimum(tree)


def __Minimum(currentNode, currMin=999999):
    numOfBranches = len(currentNode) // 2
    for i in range(numOfBranches):
        index = i * 2
        valBranch = currentNode[index]
        if valBranch < currMin:
            currMin = valBranch

        children = currentNode[index+1]
        if len(children) > 0:
            min = __Minimum(children, currMin)
            if min < currMin:
                currMin = min
    return currMin


minToFind = -90
treeToFindMin = [1,
                 [2,
                  [-5,
                   [40, [],
                    -25, []
                    ]
                   ],
                     3,
                     [9,
                      [-20, [],
                       100, []
                       ],
                      minToFind, [
                          5, [],
                          3, []]
                      ]
                  ]
                 ]

minFound = Minimum(treeToFindMin)

if minFound == minToFind:
    print("Good job!")
else:
    print("Oops, try again")

1

numOfBranches = len(currentNode) // 2

1
2
3

index = i * 2
valBranch = currentNode[index]
children = currentNode[index+1]

1
2

if len(children) > 0:
    min = __Minimum(children, currMin)

1
2

if valBranch < currMin:
    currMin = valBranch

1
2

if min < currMin:
    currMin = min

פרק הבא: