פרק קודם:

מה נלמד

• מהו מידע בינארי
• בסיסי ספירה
• מה זה byte וכמה משתנים שונים יש לנו
• איך לעבוד עם קבצים בינאריים
• The walrus operator
• הגדרת קובץ בינארי משלנו
• תכנון קוד

מידע בינארי

כמו משתנה בוליאני שמגדיר True או False.
הבסיס למידע בינארי היא יחידה קטנה שנקראת ביט - Bit.
כל ביט מכיל 0 או 1.

קבצים בינאריים

קבצי טקסט מכילים מידע שאנשים יכולים לקרוא - קבצים בינאריים אלו קבצים שמכילים מידע שרק המחשב יודע לקרוא.
או להגדיר בצורה יותר טובה - בשפה שקוד יודע לקרוא.

בסיס ספירה

כשאנחנו סופרים מספרים אנחנו משתמשים בבסיס ספירה מבלי לדעת שאנחנו עושים זאת.
במתמטיקה שמלמדים בתיכון משתמשים בבסיס ספירה 10.
זה מגדיר את כמות הספרות שאנחנו משתמשים.

1

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

בעזרת הספרות האלו אנחנו יכולים לבנות קומבינציות ספרות שנותנים לנו מספרים:

• 5
• 99
• 125
• 952034234723

וכמובן שזה אניסופי.

המשמעות המתמטית של מיקום הספרות במספרים

נדמיין שאנחנו סופרים:
…7, 8, 9…
אנחנו יודעים שמגיע 10 כי אחרי 9 מקדמים את הספרה שמאלה למספר העשרות.
במתמטיקה המיקום של הספרה מיוצג בעזרת חזקה:

1

10^1 * 1 + 0  

אם למשל לוקחים 99 אז זה:

1

10^1 * 9 + 10^0 * 1 + 9  

מה זה המספר 985?
כתבו את זה מתמטית.

1

(10^2 * 9) + (10^1 * 8) + 10^0 * 1 + 5

החוקיות פה היא לקחת את הבסיס שאנחנו נמצאים בו - בסיס 10 במקרה הזה ולבצע פעולת חזקה על המיקום של הספרה.

שיטת הספירה הבינארי - בסיס 2

לעומת בסיס 10 שיש לנו 10 ספרות להשתמש על מנת לספור, בבסיס 2 יש לנו רק 2 ספרות:
0 ו 1.

סופרים בבסיס בינארי באותו אופן שכותבים ספרות רגילות רק עם 0 ו1.

בדיחה קומית:

יש לנו 10 אנשים בעולם, כאלו שמבינים בינארית - וכאלו שלא!

תרגיל

ספרו בבינארית עד 50!

1
2
3
4
5

def ToBinary(n):  
    return bin(n).replace('0b','') 

for i in range(50):
    print(f"|{i}|{ToBinary(i)}|")

על ביטים, בייטים ועוד

המחשב מגדיר את גודל המספרים שהוא יכול לייצג כי בסופו של דבר הוא צריך לייצג את זה באופן חשמלי.
היחידה הכי קטנה במחשב 0 או 1 נקראת ביט-Bit.
בייט-Byte מורכב מ-8 ביטים.
מילה-Word מורכבת מ-2 בייטים.
מילה כפולה-DWord מורכבת מ-2 מילים.
מילה מרובעת-QWord מורכבת משתי מילים כפולות או 4 מילים.

מהו הגודל הפיזי של מילה?

גודל היחידות - בייט,מילה, מילה כפולה ומילה מרובעת תלויה במימוש של מערכת ההפעלה.
כיום רוב המחשבים הביתיים מגדירים מילה כ-64 ביטים(או 8 בייטים).
איך מייקרוסופט השאירו את הגדלים שכפי שתיארתי למעלה על מנת לא ליצור בלבול.

ניתן לקרוא כאן להעמקה בנושא

בייצוג בינארי מספר מוגדר ע”י שני מצבים בלבד ולכן בייצוג מתמטי כל ספרה מיוצגת בכפל 2 בחזקת המיקום שלו במספר.
למשל 101:

1

(1 * 2^2) + (0 * 2^1) + (1 * 2^0) = 101  

עד ל-255, המספר המקסימלי של בייט.

Hexadecimal - האקסאדצימאלי - בסיס ספירה 16

כל 4 ביטים נקראים ניבל-Nibble.
יש סיבה למה רושמים ביטים בקבוצות של 4.
מאוד נוח לייצג 4 ביטים בבסיס 16 - האקסאדצימאלי.
האקסה - 6
דצימאלי - 10

אם בסיס 10 זה 10 תווים, בסיס 2 זה 2 תווים, לכן בסיס 16 הוא 16 תווים!
התווים שמשתמשים בהם:

1

0 1 2 3 4 5 6 7 8 9 A B C D E F

למה כל כך נח להשתמש ב-הקסאדצמיאלי כדי לייצג מידע בינארי?

בייטים גודלם 8 ביטים.
מהסיבה הזו מאוד נוח לייצג בייט אחד עם 2 ספרות הקסאדצימאליות.
לאדם יהיה הרבה יותר גם לקרוא אותיות ומספרים מאשר מספרים ארוכים שכוללים 0 ו-1.

למשל המספר 44,979:
בבינארי זה יהיה:

1

1010 1111 1011 0011

והקסאדצימאלי זה יהיה:

1

AFB3

הרבה יותר קומפקטי ונוח.
דוגמא נוספת זה ייצוג של צבעים, לצבעים יש קוד הקסאדצימאלי שנוח יותר להעתיק אותו ולכתוב.

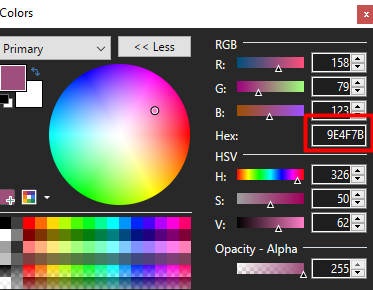
תרגילים לספירה

1.
אם תפסתם את קונספט הספירה עוד ממקודם אז תנסו לספור לבד מ-17 עד 50!

2. השלימו את המספרים:

   בסיס 10	בסיס 16
   37
   99
   112
   960

1
2
3
4
5
6
7

def ToBinary(n):  
    return bin(n).replace("0b", "") 
def ToHex(n):  
    return hex(n).replace("0x", "") 

for i in range(50):
    print(f"|{i}|{ToBinary(i)}|{ToHex(i)}|")

מחשבון מתכנתים

קודם כל - למחשבון של ווינדוס יש מוד למתכנתים שעוזר לכם להתמודד עם כל הספירה הזו:

דוגמא לשימוש במחשבון:

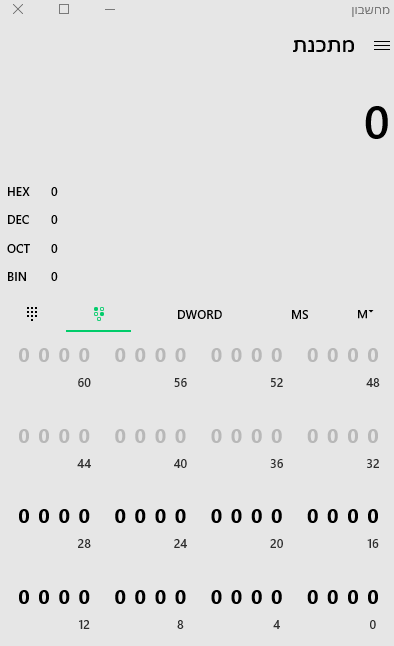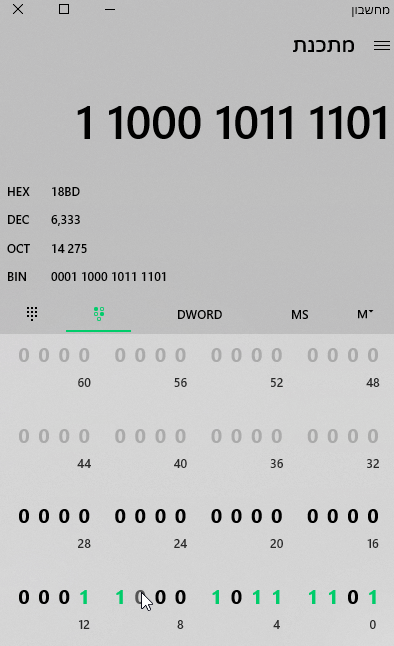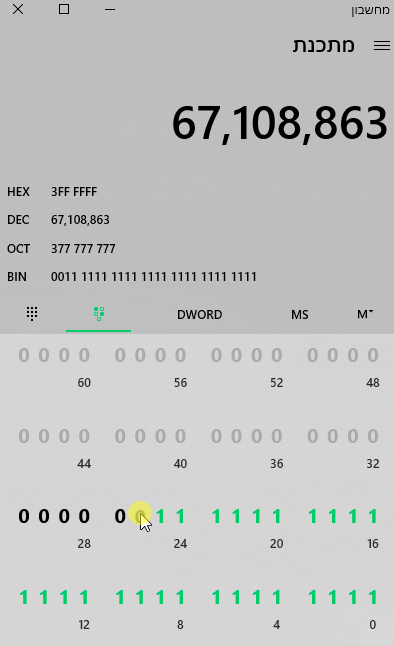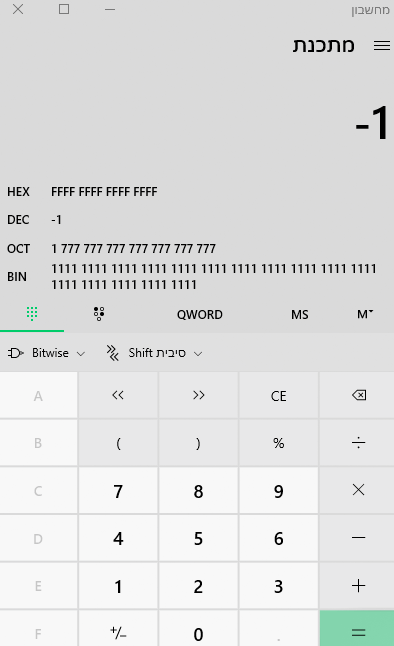
תלמדו להשתמש במחשבון הזה - בתור מישהו שעובד הרבה עם ביטים ובייטים אני משתמש בו הרבה פעמים.

Unsigned - Signed

הביטויים מתייחסים למספרים שליליים וחיוביים.
unsigned מתייחס למספרים חיוביים בלבד - 0 ומעלה.
signed מייתחס למספרים שליליים, חיוביים ו0.

אז איך בעצם אנחנו מייצגים מספר שהוא שלילי?
בצורה מאוד פשוטה - משתמשים בביט האחרון או הכי שמאלי!
1 זה מינוס, 0 זה חיובי.

שיטת המשלים ל-2

יש ייצוג אחר למספרים שליליים שעוזרים לנו גם לבצע פעולות מתמטיות בצורה פשוטה יותר.
אני לא ארחיב על זה יותר מדי כי זה לא חובה לדעת.
לעוד מידע על זה ניתן לקרוא פה:
משלים ל-2

Endianity - מה מגיע קודם

הביטוי מתייחס לסידור הבייטים.
נניח יש לנו מספר גדול:

1

322945 = 0000 0100 1110 1101 1000 0001

או שנוכל לכתוב אותו ככה:

1

322945 = 0001 1000 1101 1110 0100 0000 

מה השתנה כאן?

יש לנו שני מושגים שונים:

• Little Endian
• Big Endian

Little Endian מתייחס לסידור שהביט הכי קטן הוא קודם.
Big Endian מייתחס לסידור שהביט הכי גדול הוא קודם.

ז”א בדוגמא שכתבנו:
Big Endian:

1

322945 = 0000 0100 1110 1101 1000 0001

Little Endian:

1

322945 = 0001 1000 1101 1110 0100 0000 

לביט הכי קטן והכי גדול יש מושגים משלהם:
Most Significant Bit - MSB
Least Significant Bit - LSB

תרגיל

תכתבו את המספרים הבאים בבינארית באינדיאניטי קטן וגדול:

איך זה משפיע על הקוד שלנו?

אתם כותבים פרוטוקול בינארי, הקוד שלכם מקבל 4 בייטים, מבלי לדעת את הסדר הנכון של הבייטים האלו איך תוכלו לדעת מהו המספר האמיתי?

בצורה אינטואיטיבית נחשוב שדווקא - Big Endian הוא הלוגי יותר.
כי השכל שלנו רגיל לקרוא מימין לשמאל מספרים.
(שהימין הוא הקטן ביותר).

אך יש מערכות - או יותר נכון היו - שעובדים בעזרת Little endian.
הסיבות די מורכבות אך אחת הטענות היא שמבחינת זיכרון קל יותר לטעון מספרים שהם Little endian.
אני לא אכנס פה לפרטים כי צריך לדעת Assembly.

קוד פייתון

אחרי שסקרנו בהרחבה,
אנחנו מוכנים לעבוד בקבצים בינאריים בפייתון!

בפרק הקודם הגדרנו פרוטוקול בינארי שנרחיב אותו בפרק הזה.

להלן הקובץ שלנו, חילקנו אותו לשורות כדי שיהיה נוח להסתכל בו:

1
2
3
4
5
6
7
8
9
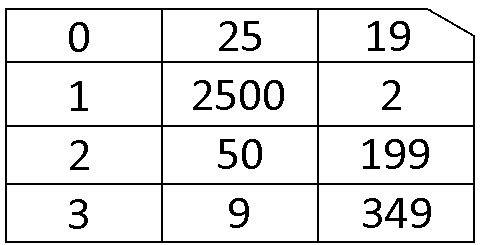
10

arr = [0, 25, 19, 1, 2500, 2, 2, 50, 199, 3, 9, 349]
with open("binaryFile", "wb") as file:
    for num in arr:
        bytes = num.to_bytes(4, "big")
        file.write(bytes)

with open("binaryFile", "rb") as file:
    while (bytes := file.read(4)) :
        number = int.from_bytes(bytes, "big")
        print(number)

אנחנו מגדירים כל שורה במערך באופן סדרתי כי ככה קבצים עובדים - הם כתובים כמקשה אחת.

על := במקשה אחת

שימו לב לשורה 7 בקוד הקודם.
ה-while השני נראה מעט מוזר.
הפרמטר := מאתחל משתנה במקשה אחת ביחד עם ה-while.
אם כמות הבייטים תהיה שווה ל-0 תנאי הלולאה לא יתקיים.
זה כמו לכתוב את הקוד בצורה:

1
2
3
4
5
6

with open("binaryFile", "rb") as file:
    bytes = file.read(4)
    while (bytes != 0) :    
        number = int.from_bytes(bytes, "big")
        print(number)
        bytes := file.read(4)

רואים כמה זה חוסך לנו?
האופרטור הזה נקרא גם The Walrus Operator.

פונקציות פייתון לקריאת קבצים בינאריים

על מנת לקרוא או לכתוב קובץ בינארי צריך להוסיף -b.

1
2

writeBinaryFile = open('file.bin','wb')
readBinaryFile = open('file.bin','rb')

יש לנו שני פונקציות ש-int נותן לנו כדי לעבוד עם בייטים:

1
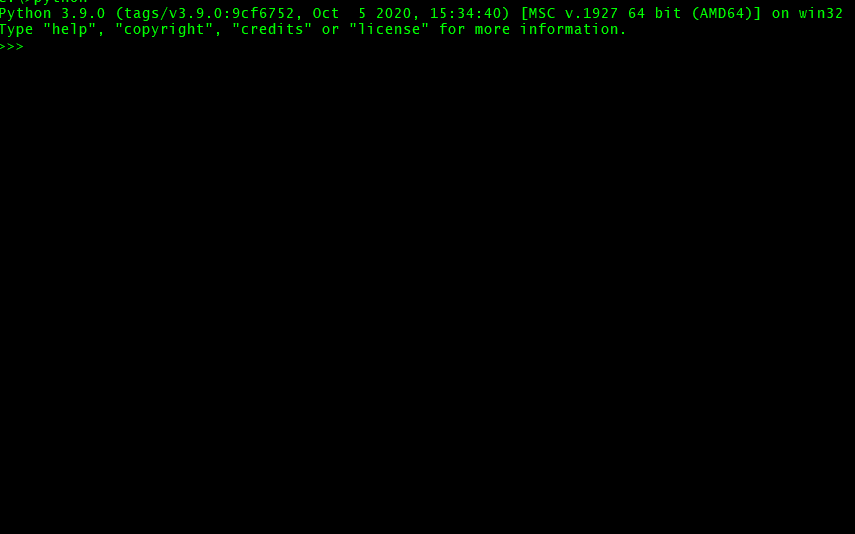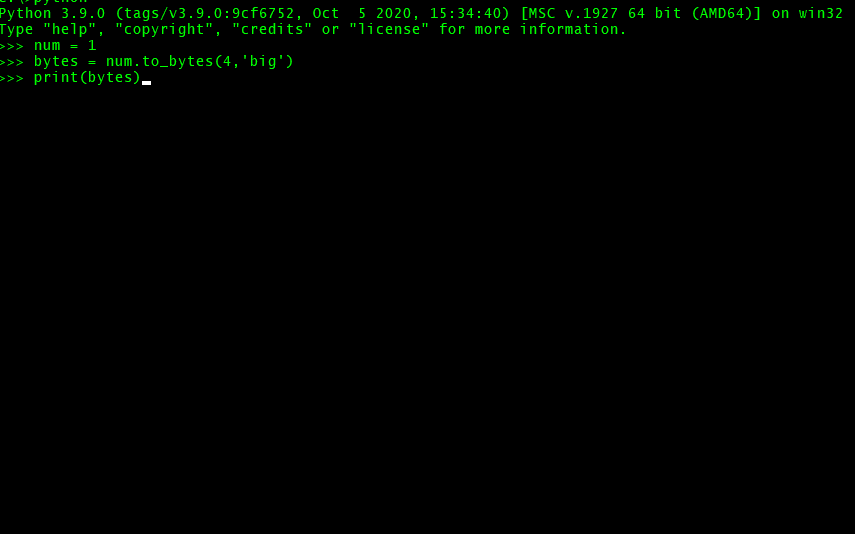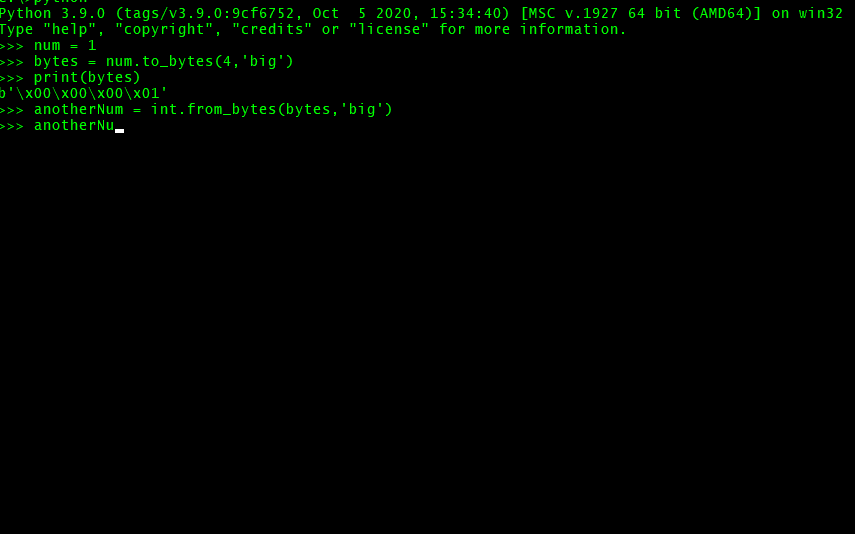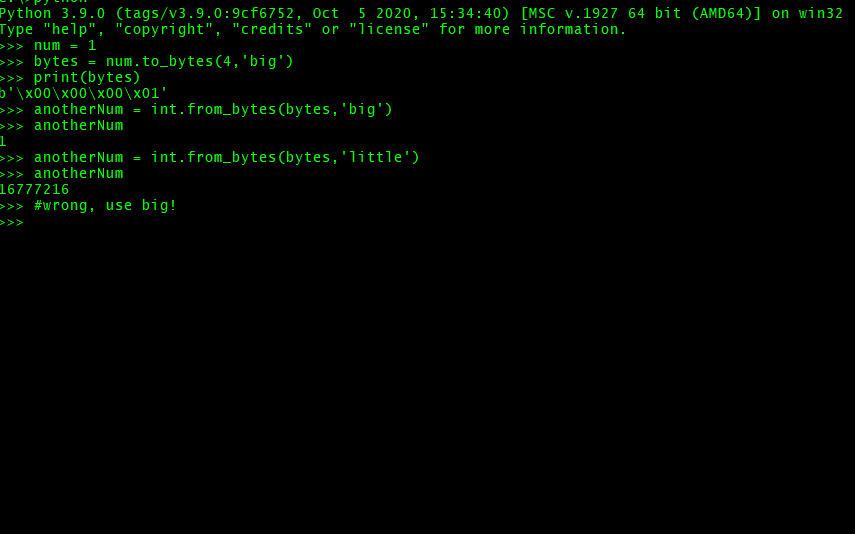
2

to_bytes(num_of_bytes_to_generate, endianity)
number = int.from_bytes(bytes, endianity)

endianity יכול להיות 'big' או 'little' כפי שלמדנו למעלה.

num_of_bytes_to_generate מחליט כמה בתים לייצר עבור המספר.
אם נביא לו את הערך 1 אך נבקש ממנו לייצר 4 בייטים זה יצור לנו:

1
2
3

num = 1
print(num.to_bytes(4,'big'))
#0 0 0 1

bytes - זהו משתנה בתים מיוחד.

בפייתון הסוג המשתנה המיוחד שמטפל ברשימה של בייטים הוא - bytearray.
השימוש בו הוא נורא פשוט, הוא כמו רשימה רגילה שאתם כבר מכירים:

1
2
3
4
5
6

bytes = bytearray([0,0,0,1,2,255])
for byte in bytes:
    print(byte)

string = "SimpleCode"
bytesForString = bytearray(string, 'utf-8')

שימו לב: לא ניתן לשים בבייטים מספר שגדול יותר מ255.
הרשימה bytearray לא ניתן לשנות.
אם רוצים סוג שניתן לשנות ניתן ליצור רשימה עם bytes, אך אני לא ממליץ על זה אלה אם כן אין ברירה.
לכן אנחנו נעבוד עם bytearray.

הדגמה:

מהו פרוטוקול

פרוטוקול הוא הגדרת חוקים לצורה שבה אנחנו מעבירים מידע או מייצגים מידע.
למשל אם ניקח סדרת מספרים רנדומלית:
[1,2,3,4,5]
הם לא יגידו לנו כלום, האם הם אינדקסים למערך אחר? האם זה כמות של מוצרים? האם זה הגדרה של סדרה?
רק פרוטוקול שמוגדר היטב יוכל לומר לנו מהו המידע.

זוכרים שאמרנו שמידע בינארי הוא לא עקבי אלה אם כן אנחנו יודעים בוודאות מה הוא מכיל?
עבור המטרה הזו צריך להגדיר פרוטוקול שיגדיר מה כל מספר מייצג.

פרוטוקול רשימת מוצרים

• כל מספר יהיה בגודל 4 בתים(בייטים) ללא מספרים שליליים.
• כל 3 מספרים מייצגים מספר - משמע 12 בייטים

  מיקום	משמעות	מיקום בייט
  0	מזהה	0
  1	כמות במלאי	4
  2	מחיר ליחידה בודדה	8

בתמונה רואים שיש 24 בייטים סך הכל:

מוצר ראשון - בייט 0 עד 11

מוצר שני - בייט 12 עד 23

• גודל תקני של קובץ יוגדר באופן הבא:

1
2
3

BytesInNum = 4
NumOfBytesInRow = 3
IsValid = FileSize % ( NumOfBytesInRow * BytesInNum ) == 0

• כפילויות:
  הפרוטוקול ייאפשר כפילויות בין מוצרים - ז”א מזהה מוצר יכול להיות זהה למזהה מוצר אחר.

הגדרת API

כדי להיות חכמים ולהגדיר מראש כיצד אנחנו נקרא ונכתוב בפרוטוקול לכן נגדיר פונקציות.
הפונקציות האלו נקראות - Application Programming Interface.
כמו שיש לנו ממשק משתמש שניתן ללחוץ על כפתורים כדי לבצע פעולות,
יש לנו ממשק מתכנת - פונקציות וכלים אחרים שנותנים למתכנת גישה לפעולות.

הצעד הראשון זה להגדיר עם איזה מידע אנחנו עובדים - מה ה-Input ומה ה-Output.
הצעד השני זה להגדיר שמות ברורים.
והצעד השלישי זה לכתוב את התכנון כיצד להשתמש בפונקציות.

נתחיל מהמידע שאנחנו עובדים איתו - איזה פרמטרים בעצם נרצה.
תחשבו מעט לפני שאתם פותחים את התשובה.

1

products = [[0,2,3], [1,20,50],[0,953,5]]

הצעד השני אמרנו הוא להגדיר את הפונקציות, חשבו על שמות מתאימים:

וכעת נתכנן את השימוש בפונקציות.
בשלב הזה אנחנו מגדירים את החתימה של הפונקציה - מה היא מקבלת, מה היא מחזירה.

נוכל לזרז תהליכים ופשוט לכתוב בפייתון:

1
2
3
4
5
6
7
8

def ValidateProducts(bytes):
  pass

def ReadProducts(bytes):
  pass

def WriteProducts(array):
  pass

שימו לב שלא מימשנו עדיין כלום - בשלושה שלבים אנחנו הגדרנו מה המידע שלנו, מהם השמות של הפונקציות וכיצד הם נראים.
עכשיו לחלק הפחות כיף - המימוש.

מימוש

נתכנת את המימוש בעזרת מתודולוגיית פיתוח שנקראת - Test Driven Development.

גישות תכנון ותכנות

יש בתעשייה כל מיני תפקידים בתכנות - חלקם משפיעים יותר על התכנון וחלקם פחות.
מה שבטוח זה שלמתכנתים בדרך כלל יש הרבה השפעה וחופש על כיצד הם מתכננים את העבודה שלהם וכותבים את הקוד.
הסיבה העיקרית לזה שזה התפקיד של מתכנתים בסופו של יום זה לדעת כיצד לתכנן, לכתוב ולהוציא קוד לאור.

מתכנתים טובים שואפים להכיר כמה שיותר בתכנון וכתיבה של קוד

בגישת ה-Test Driven Development אנחנו כותבים קודם כל קוד שבודק את הקוד שאנחנו הולכים לכתוב.
למשל, נתון לנו הקוד הבא:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def Add(a, b):
    return 0


# Testing:
testingData = [[1, 2, 3], [5, 5, 10], [6, 10, 16]]

for data in testingData:
    a = data[0]
    b = data[1]
    expected = data[2]

    result = Add(a, b)
    if result != expected:
        print(f"Fail! a:{a} b:{b} result: {result}")
    else:
        print(f"Pass! a:{a} b:{b} result: {result}")

שימו לב לפונקציה שאנחנו בודקים - לא מימשנו אותה!
בגישת התכנות הזו - אנחנו קודם מממשים את הקוד שבודק את הקוד שלנו ואחר כך אנחנו מממשים את הקוד שלנו.

תרגול

1.
תריצו את הקוד מבלי לממש את פונקציית החיבור.
2.
ממשו את פונקציית החיבור ותריצו את הקוד.

1
2
3

Fail! a:1 b:2 result: 0
Fail! a:5 b:5 result: 0
Fail! a:6 b:10 result: 0

1
2
3

Pass! a:1 b:2 result: 3
Pass! a:5 b:5 result: 10
Pass! a:6 b:10 result: 16

הטסטים לפרוטוקול הבינארי:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

def ReadProducts(bytes):
    pass


def ValidateProducts(bytes):
    pass


def WriteProducts(products):
    pass


# Tests
################## Validate products ##################
# Bytes contains the numbers (1,20,25) 4 bytes per each
bytesToValidate = bytearray([0, 0, 0, 1, 0, 0, 0, 20, 0, 0, 0, 25])
isValid = ValidateProducts(bytesToValidate)
if isValid:
    print("Validate Products Pass")
else:
    print("Validate Products Fail")
#######################################################

################## Write products ##################
products = [[1, 1, 1], [2, 2500, 9]]
expectedBytes = bytearray(
    [0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 9, 196, 0, 0, 0, 9]
)
writeBytes = WriteProducts(products)
# Bytes should be 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 2 0 0 9 196 0 0 0 9
if writeBytes == expectedBytes:
    print("Write Products Pass")
else:
    print("Write Products Fail")
###################################################

################## Read products ###################
bytesToValidate = bytearray([0, 0, 0, 1, 0, 0, 0, 20, 0, 0, 0, 25])
expectedProducts = [[1, 20, 25]]
afterReadProducts = ReadProducts(bytesToValidate)
areSame = afterReadProducts == expectedProducts
if areSame:
    print("Read Products Pass")
else:
    print("Read Products Fail")
###################################################

אם תריצו את הקוד הזה אז אתם תראו שהכל נכשל.
כעת ניתן לממש את הפונקציות כדי שייעבדו.

מימוש הפרוטוקול

ממשו את הפרוטוקול.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

def ValidateProducts(bytes):
    # כמות הבתים שיש לנו
    length = len(bytes)
    # אם החלוקה ב-12 נותנת לנו 0 אז הבתים תקינים
    return length % (12) == 0


def ReadProducts(bytes):
    # קודם אנחנו מגדירים את המשתנים שייעזרו לנו בחישובים שלנו
    endianity = "big"

    # כל 12 בייטים זה 3 מספרים למוצר אחד.
    # לכן כדי לחשב את כמות המוצרים אנחנו צריכים לחלק את כמות הבייטים ל-12.
    length = len(bytes)
    productsNumber = int(length / 12)

    # אנחנו צריכים לקפוץ 12 בייטים בין כל מוצר
    # ולקפוץ 4 בייטים עבור כל מספר בודד כמו שהראנו בהגדרת הפרוטוקול
    products = []
    for i in range(productsNumber):
        # כל מספר ברשימה הוא 4 בתים, מוצר מגדיר 3 מספרים ולכן זה 12 בייטים!
        # המוצר הראשון 0, השני 12 השלישי 24 וכדו
        startOffset = i * 12
        # [:] מבצע חיתוך מהמערך
        # חותכים מהמיקום שאנחנו נמצאים את המזהה ה-4 בייטים הראשונים.  
        id = int.from_bytes(bytes[startOffset : startOffset + 4], endianity)
        # אחר כך קופצים 4 בייטים קדימה כדי לקרוא את הכמות של המוצר
        amount = int.from_bytes(bytes[startOffset + 4 : startOffset + 8], endianity)
        # בסוף אנחנו קוראים את ה-4 בייטים האחרונים עבור המחיר
        price = int.from_bytes(bytes[startOffset + 8 : startOffset + 12], endianity)
        # אנחנו מוסיפים למערך את המספרים שהוצאנו
        # זכרו שזה מערך של מערכים ואנחנו מאפשרים כפילויות
        products.append([id, amount, price])
    return products


def WriteProducts(products):
    # לפי הפרוטקול כל מספר הוא 4 בייטים ומשתמשים ב-big.  
    numOfBytesPerInt = 4
    endianity = "big"

    # רשימה של בייטים משתמשים במשתנה bytearray.  
    # הסוגריים יוצרות אחד חדש
    bytes = bytearray()
    # יש רשימה של רשימות לכן רצים פעמיים
    for product in products:
        for property in product:
            # לוקחים את המספר שיש לנו ברשימה ומוציאים את הבייטים - זו גם רשימה
            propertyBytes = property.to_bytes(numOfBytesPerInt, endianity)
            # מכיוון שזה גם רשימה אנחנו רצים עליו עם לולאה ומסיפים לרשימה הראשית של הבתים
            for byte in propertyBytes:
                bytes.append(byte)
    return bytes


# Tests
################## Validate products ##################
# Bytes contains the numbers (1,20,25) 4 bytes per each
bytesToValidate = bytearray([0, 0, 0, 1, 0, 0, 0, 20, 0, 0, 0, 25])
isValid = ValidateProducts(bytesToValidate)
if isValid:
    print("Validate Products Pass")
else:
    print("Validate Products Fail")
#######################################################

################## Write products ##################
products = [[1, 1, 1], [2, 2500, 9]]
expectedBytes = bytearray(
    [0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 9, 196, 0, 0, 0, 9]
)
writeBytes = WriteProducts(products)
# Bytes should be 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 2 0 0 9 196 0 0 0 9
if writeBytes == expectedBytes:
    print("Write Products Pass")
else:
    print("Write Products Fail")
###################################################

################## Read products ###################
bytesToValidate = bytearray([0, 0, 0, 1, 0, 0, 0, 20, 0, 0, 0, 25])
expectedProducts = [[1, 20, 25]]
afterReadProducts = ReadProducts(bytesToValidate)
areSame = afterReadProducts == expectedProducts
if areSame:
    print("Read Products Pass")
else:
    print("Read Products Fail")
###################################################

ראינו שפרוטוקול בינארי עד כמה שהוא מורכב יכול להיות פשוט כאשר אנחנו מפרקים אותו לגורמים.
למדנו מה זה ספירה בינארית, כיצה לפרש מספרים בעזרת הקסאדצימאל ולכתוב קוד שקורא וכותב מידע בינארי.

בפרק הבא נעבור על פורמט פופולרי - JSON!